昨天看到曾经获得理论物理博士学位，现在在做应用研究开发的“吊床物理学家”Johannes Koelman的博文：Holographic Dark Universe

该博文讨论全息暗能量。打开一看，我本来以为他有什么新想法，原来还是类似2000年Scott Thomas就有的想法。

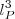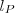先看量子场论是如何估计真空能量密度的。在量子场论中，一个最小的空间胞的体积是，其中是普朗克长度。普朗克长度出现在这里很“自然”，因为单从量子场论的角度看，我们没有理由不相信普朗克长度是量子场论成立的最小尺度。如果我们认为的确可以有这个最小空间体积，那么在这个体积中的一个量子的最大能量是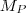，其中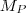是普朗克质量，在自然单位制中，能量密度就是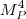，一个非常大的量。

那么，宇宙学观测告诉我们什么？暗能量或真空能量密度和临界密度是一个量级，也就是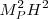，H是哈勃常数。哈勃常数比普朗克质量小大约60个量级，所以量子场论允许的真空能密度比观测值大120个量级，这就是Koelman嘴里的物理学家们的euphemistic statement：宇宙学常数问题。我想起翟永明的一本书，叫《最委婉的词》，宇宙学常数问题是物理学家最委婉的提法吧。

用Koelman的形象说法，暗能量密度大约是一个一千公里立方体内含有一个普朗克能量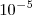（克）。

将公式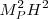中的一个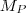变成普朗克长度倒数，H变成宇宙大小L的倒数，这个公式告诉我们，在体积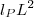之内，有一个普朗克能量。我们再看Koelman如何建议从量子场论的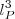过度到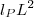的。这需要将两个普朗克长度因子变成两个宇宙尺度因子。第一步，根据全息原理，宇宙中的自由度个数不是一个宇宙体积含有很多普朗克体积，即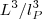，而是Bekenstein-Hawking自由度个数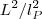，这样，我们就将一个普朗克长度变成了宇宙尺度。进一步，每个自由度的能量不该是普朗克能量，而是其Compton波长为宇宙尺度的能量，这样就将第二个普朗克长度换成宇宙尺度。这个想法，早在2000年，Scott Thomas已经有了。而我们最近的全息气体的想法，就含有这个建议。

在这个全息图像中，自由度个数是BH熵我们觉得相对容易接受一点，这等于说自由度可以由宇宙学视界来描述，视界的面积被分成边长为普朗克长度的元胞。相对难以接受的是，一个元胞中的零点能不是普朗克质量而是宇宙尺度的倒数，后者是一个非常小的量。一个可能的解释是，从宇宙学视界到作为观测者的我们有一个很大的红移，是这个红移因子将普朗克质量压低了。的确，我们可以用所谓的stretched horizon来解释这个红移因子。

如果Koelman是独立发现这个想法的，我的理解是一个好想法总是被不断地重新发现，也许全息暗能量就是这样一个好想法。

全息暗能量的根据是全息原理。在宇宙学中，全息原理的一个困难是如何从那些微小的量子（能量只有宇宙尺度的倒数）构造出丰富多彩的宇宙。这就是所谓从非局域到局域的问题，全息原理如果想进步，必须解决这个问题。我们需要新概念，毫无疑问。

那么，最近流行的Horava理论是否含有这样的新概念？看上去不那么乐观。我和庞毅的工作也许指向Horava理论是一个拓扑理论，这也许是到全息原理的第一步。

我还有一个更加怪诞的建议，我们的宇宙通过全息原理不仅是两维的，甚至是一维的！这话怎么讲？还是回到暗能量密度，如果世界是一维的，那么只有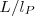个自由度，此时，为了得到足够大的能量。每个自由度的能量不再是宇宙尺度的倒数，而是普朗克能量。

也许你会反驳，一维的自由度太少了，只有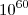，还没有微波背景辐射的自由度多，你是正确的，微波背景辐射的自由度大约是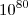。这不要紧，这里我们不想解释整个宇宙，我们只想解释暗能量含有的自由度，如果暗能量的自由度是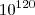，我觉得有点太浪费，因为这个数不仅远大于微波背景辐射的熵，也远大于宇宙中所有黑洞含有的熵。

若干年前，我和两位学生写过一篇文章One conjecture and two observations on de Sitter space，其中就出现过一维（1+1维）理论，最近，Strominger和宋伟等人在四维Kerr黑洞中，也看到了一维理论，所以，一维理论也不是不可能的。

只有时间才会告诉我们什么是正确的。

——————————————————————–

27号凌晨，看到有从一个韩国博客来的访问，点击看过去，是一篇用韩文谈论我和庞毅文章的博文，文章后贴了一条龙，来自中国的恶龙吧 :-）

韩文及google中文翻译如下：

북경에서 온 통신 - HL 죽이기

이러면 꼭 북경에 비밀리에라도 아는 사람이 있는 것처럼 들릴지도 모르지만, 사실은 화요일에 아카이브에 뜬 다음 논문에 대한 이야기다.

http://arxiv.org/abs/0905.2751

저 자는 두 사람이지만 중요 저자는 당연히 미아오 리. 소속은 중국 과학 아카데미(中國科學院)의 이론물리 연구소. 내가 과문한 탓이겠지만 중국에서 나온 논문을 꽤나 긴장하며 읽기는 오랫만이다. 이 논문의 제목은 “Horava-Lifshitz 중력의 문제점(A Trouble with Horava-Lifshitz Gravity)”. 리 스몰린이 끈이론을 비판한 책인 “물리학의 문제(The Trouble with Physics)”가 연상되는 것은 나만의 생각일까.

이 논문의 저자가 구체적으로 살펴보고자 하는 것은 HL이론의 재규격화 문제. 호자바는 일단 급수를 세는 것만으로 재규격화가 가능할 것으로 상정했지만, 실제로 게이지 이론, 혹은 더 일반적으로 말해 제한조건(constraint)가 있는 고전 이론의 양자화에는 미묘한 점이 많다. 제한조건이 게이지 대칭성과 연관되어 있다면 결국 괜찮다는 것이지만, HL이론이 어차피 중력이론을 지향한다면 당연히 아인슈타인 이론과 마찬가지로 에너지 제한조건, 운동량 제한조건이 성립해야 하는데, 이것은 고전적으로 중력계의 에너지나 운동량을 계산하면 항상 0이 나오는 결과를 낳게 된다. 문제는 HL이론의 경우 이 제한조건들을 양자화하기 위해 포아송 괄호를 계산하게 되면 새로운 제한조건이 계속 나온다는 것. HL이론의 포텐셜 부분이 복잡하기 때문에 꽤나 따분한 계산을 했을 텐데, 이 저자들의 결론은 제한조건이 너무 많아 결국 위상공간이 남아나지 않는다는 것. 또는, 단순히 논리적이기만 한 결론이지만, 위상 공간이 홀수 차원이라 제대로 된 상사구조를 줄 수 없다는 것. 물론 위상공간이 남아나지 않는다는 것은 바로 중력자가 생기지 않는다는 것을 의미하기 때문에, “중력을 재규격화가 가능하도록 수정했더니 더 이상 중력 이론이 아니더라”라는, 데자뷰가 느껴지는 결론을 얻게 된다.

google翻译：

通讯从北京- HL杀死

你知道你有秘密，因为它在北京的声音，但实际上留在存档周二就该报补充说。

http://arxiv.org/abs/0905.2751

作者是两个人，但当然作者miahoh李。在中科院（中国科学院）理论物理研究所。我来自中国gwamunhan tatyigetjiman有很长一段时间我读了一份文件，是非常紧张。 “Horava-Lifshitz (A Trouble with Horava-Lifshitz Gravity)”.的标题，论文“荷拉伐，里夫施茨问题的严重性（故障与荷拉伐，里夫施茨重力） ” 。(The Trouble with Physics)” 小kkeunyironeul琳李批评页面“物理问题（故障与物理） ”我的想法是，旧的。

具体来说，笔者想看看HL理论 jaegyu恶化的问题。 (constraint) JOSAS酒吧，只是一个伯爵的水将提交给战争，但jaegyu事实上，规范理论，也就是说，或更普遍的限制（约束）量化的经典理论是一个微妙的一点。 对称性限制和衡量连接到年底，但没关系，反正HL理论，当然，如果重力导向理论，爱因斯坦的理论和能源的制约因素，制约因素，必须建立的势头，这在古典严重性，系统计算出的能源或动力结果总是0 。 如果限制了HL理论，量子化条件poahsong括号的计算时，新的限制将继续下去。 由于复杂的理论potensyeol了HL计算将有一个相当乏味，作者的结论是太多的限制不会结束，而不是其余的相空间。 或者，只是一个合乎逻辑的结论，但yigiman ，相空间是奇数维工作将无法提供了坚实的结构。 相空间仍然存在，当然，这并不意味着它不只是发生严重的“严重性的战争可以进行修改，以jaegyu理论的重心，而不是当我不再是”一个，结论将能够感觉到 。

然而，相空间，一方面是丢失， 很久以前，奥兰多- repeoteu文件，如理论，反正jaegyu HL与加剧三维阶段potensyeol jaegyu的严重性取决于战争的实力，我接受没有自由去，不能正常工作，所以我想惊讶。