所有数学问题，可以分为两类，一类是确定性问题，如一个一元二次方程的解可以套用公式。另一类是非确定性问题，不存在一个普遍公式可以套用，如决定一个整数是否是素数。

P问题：确定性问题，同时可以通过图灵机在多项式时间内解决的问题。

NP问题：非确定问题，其任何给定回答可以在多项式时间内验证是否正确。特别注意这里用了“给定”两个字。

NP与P的最大区别是你必须先猜一个解答，然后去验证。

一个没有解决的难题是，P作为P问题的集合是否等于NP作为NP问题的集合，及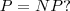

这个问题被Clay数学研究所列为7个大奖问题之一。

最近，印度数学家Vinay Deolalikar声称解决了这个问题，他的个人主页。

他的论文长达66页，题目是”P is not equal to NP“，已经在八月六日送给一些同行。这篇文章的概要。

过去，人们为了解决这个问题，发明了所谓NP完全问题，NP-complete或NPC是NP一个子集，可以看成NP中最难的问题，其定义是，所有NP中的问题都可以在多项式时间内转换成NPC中的任何问题。

木遥在他的博客中介绍了过去一周很多专家在网上讨论的结果，看来这个证明不成立。木遥的文章。

我是外行，上面如果说错了什么请大家指出。

另外，明天国际数学家大会就要开幕了，有人在网上猜测有三位数学家将获得菲尔兹奖，其中Ngo Bao Chau是越南教授（真正在越南教书哦），Artur Avila是巴西教授，Cédric Villani是法国人。巴西人Avila最年轻，只有31岁。

Ngo Bao Chau今年38岁，主要数学成就是证明Langlands纲领中的主引理（fundamental lemma），2005年获得Clay研究奖，2009年因这个工作被时代周刊评为当年十大科学发现之一。祝愿他能够获得菲尔兹奖。