一段时间以前，忘了具体时间了，大约是凝聚态物理进入AdS/CFT专家们的视野的时候，我和学生聊天时说，下面该轮到光学了。前天，第一篇全息光学的文章出现了。

当然，全息的概念本来来自于光学，这里全息的意思是用全息原理研究给定物理系统，也就是说，用一个等价的引力理论来研究该系统。全息光学，就是用一个等价的引力系统研究光学。假如光学的空间是三维的，那么引力就是4+1维的。

这篇文章针对这些年来出现的超颖材料，具体的是负折射率的材料：

Holographic Optics and Negative Refractive Index

我对超颖材料发生兴趣，主要不是隐身衣的可能，而是用超颖材料模拟引力场，特别是宇宙学。这和全息光学正好是相反的方向，全息光学是用引力研究光学，而且是高一维的引力理论。

Amariti等人的文章只研究一个具体的情况：介电常数和磁化率作为矩阵，只含有横向部分和纵向部分，具体的就是，作为频率和波矢的函数，有

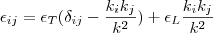
（作为3乘3对称矩阵，更一般地有6个参数）

如果将横向部分展开，有

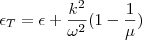
应用到Maxwell方程，有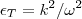，近似有

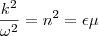
这就是折射率n的定义。当介电常数和磁化率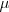都是正的时，折射率是正的，但当其中之一是负的时，折射率是纯虚数，也就是说介质是不透明的。可以设想，我们制造出介电常数和磁化率都是负的介质，我们就得到折射率为负的介质。

如果介电常数和磁化率含有虚部，也可以定义负折射率。折射率的正负可以通过以下量判定：

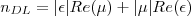
如果以上量是正的，那么折射率就是正的，反之折射率是负的。

在Amariti等人的考虑中，流体对应的引力理论中含有电磁场，这不是流体中的电磁场，是4+1的电磁场，而流体中不一定有电磁场。但流体中存在整体电流，这种整体电流可以假想和3+1维的电磁场耦合这样就可以定义折射率了。

流体的性质是什么？通过对偶的引力理论决定。他们假定4+1维中存在一个带有电荷的黑洞，这样就存在一个温度，同时存在一个化学势。这两个量决定了边界上流体的性质。

接着，通过解4+1中的Maxwell方程，决定边界理论中的流-流推迟Green函数，推迟Green函数的形式是

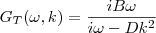
其中B和D决定了介电常数和磁化率：

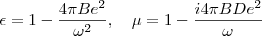
从这些公式我们看到，这种介质是耗散的，并不是实验室中已经实现的那种负折射率材料。

转发到新浪微博