有一次组会前我遇到北大的马伯强老师，问他何以有那么大兴致聊天，原来他在介绍Benford定律和他在这方面相关的工作。

什么是Benford定律？百度百科这么说：

1935年，美国的一位叫做本福特的物理学家在图书馆翻阅对数表时发现，对数表的头几页比后面的页更脏一些，这说明头几页在平时被更多的人翻阅。

本福特再进一步研究后发现，只要数据的样本足够多，数据中以1为开头的数字出现的频率并不是 1/9，而是30.1%。而以2为首的数字出现的频率是17.6%，往后出现频率依次减少，9的出现频率最低，只有4.6%。

本福特开始对其它数字进行调查，发现各种完全不相同的数据，比如人口、物理和化学常数、棒球统计表以及斐波纳契数列数字中，均有这个定律的身影。

1961年，一位美国科学家提出，本福特定律其实是数字累加造成的现象，即使没有单位的数字。比如，假设股票市场上的指数一开始是1000点，并以每年10%的程度上升，那么要用7年多时间，这个指数才能从1000点上升到2000点的水平；而由 2000点上升到3000点只需要4年多时间；但是，如果要让指数从10000点上升到20000点，还需要等7年多的时间。因此我们看到，以1为开头的指数数据比以其他数字打头的指数数据要高很多。

马伯强老师对我介绍道，全世界200个左右国家地区，如果我们看面积的第一个数字出现的频率，1到9也遵守Benford定律，同样，这些国家地区的人口的第一个数字也遵守Benford定律，这是一件很奇妙的事情。

我们看看wiki是怎么介绍Benford定律的：

Benford’s law, also called the first-digit law, states that in lists of numbers from many (but not all) real-life sources of data, the leading digit is distributed in a specific, non-uniform way. According to this law, the first digit is 1 almost one third of the time, and larger digits occur as the leading digit with lower and lower frequency, to the point where 9 as a first digit occurs less than one time in twenty. This distribution of first digits arises whenever a set of values has logarithms that are distributed uniformly, as is approximately the case with many measurements of real-world values.

This counter-intuitive result has been found to apply to a wide variety of data sets, including electricity bills, street addresses, stock prices, population numbers, death rates, lengths of rivers, physical and mathematical constants, and processes described by power laws (which are very common in nature). The result holds regardless of the base in which the numbers are expressed, although the exact proportions change.

It is named after physicist Frank Benford, who stated it in 1938, although it had been previously stated by Simon Newcomb in 1881.

有人可能会问，如果我们改变单位制呢？Benford定律恰恰是因为改变单位制而分布不变所引起的对数律。有人会继续问，如果我们改变进位制呢？例如8进位而不是10进位，甚至是2进位？Benford定律在不同进位制下的准确的表述是，在b进位制中，首位数字取d（=1,……, b-1）的几率是

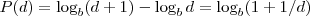
这个定律可以用来检查是否有人做了假账。通常的账本会满足Benford定律，而做了假账的账本不满足，4和5出现的频率更大，而不是1。

马伯强老师和他的学生邵立晶最近在这方面写了三篇文章，他们发现了：

1、强子的宽度遵守这个定律（文章见这里）。

2、脉冲星的重心周期满足修正的Benford定律。

3、统计物理的三个重要分布，Boltzmann-Gibbs分布，Bose-Einstein分布，Fermi-Dirac分布，也基本上满足Benford定律。