熵力与暴涨

最近我和庞毅考虑证明一个no-go定理：在一个暴涨区域，我们无法用Verlinde的全息想法推导出爱因斯坦方程。

证明分两部分。第一部分，如果我们不修改Verlinde原来的推导，那么在一个暴涨宇宙区域的表面，需要引入负温度，这是因为这个区域的Tolman-Komar质量是负的（相对于一个局域Killing矢量来说）。

核物理学家曾经引入过负温度，负温度看上去离谱，其实可以实现。例如，对于一个有有限个能级的系统，它的Boltzmann配分函数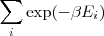是有限的。由这个配分函数定义的热力量都存在。

但负温度的引入带来很多麻烦，例如，我们在文章中指出，当一个实验粒子被虚位移到全息屏上时，能量不守恒。

解决这个问题的另一种可能是修改Verlinde的推导，即不用Tolman-Komar质量，此时，我们仍然假定温度由局域Killing矢量决定。在这个前提下，我们证明了正确的爱因斯坦方程是推不出来的。

文章见：

A No-go Theorem Prohibiting Inflation in the Entropic Force Scenario

摘要：

We show that to accommodate inflation in the entropic force scenario of Verlinde, it is necessary to introduce a negative temperature on a holographic screen, this will introduce several puzzles such as energy non-conservation. If one tries to modify the derivation of the Einstein equations to avoid a negative temperature, we prove that it is impossible to find a proper new definition of temperature to derive the Einstein equations.