一些日子前，我在Johannes Koelman的博客上读到一则有趣的故事，故事说，荷兰弦论家Erik Verlinde最近导出了引力，当然是通过全息原理。如果这故事是真的，我觉得是一个进步。我们很长时间焦虑的一件事是从所谓的量子引力导出全息原理，这种焦虑是否类似一个多世纪前Lorentz等人焦虑如何从电磁理论导出Lorentz收缩？如果我们像爱因斯坦一样，像接受光速不变原理一样接受全息原理，也许我们可以导出量子引力和经典引力，而不是相反。

可惜，Johannes Koelman并没有给出任何细节，上网查，也没有Erik Verlinde的最新文章。他今年只写了两篇文章，他本不是一个高产的人，也不随便将一篇文章抛出（惭愧，今年在我名下的文章有11篇，还有一篇正在完成中）。不过，从Johannes Koelman博客中的照片看出，Verlinde的口袋里确实有些货。

Verlinde今年的两篇文章是

A Black Hole Levitron

Holographic Neutron Stars

且慢，先不要去读这些文章，它们与从全息原理导出引力无关。

我们先看看Koelman是如何推测Verlinde的工作的。（与Koelman不同，我用单位制：k=c=hbar=1）

假定黑洞表面上有温度T，那么每个自由度有能量1/2 T，假如有N个自由度，则总能量是1/2 NT。这个能量等于黑洞的质量M。

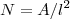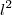接着，我们需要关于N的公式。全息原理告诉我们，，其中是一个基本面积单位。所以，我们有

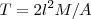
另外，根据Unruh，黑洞表面温度由加速度决定，即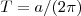，将此式与上式比较，得

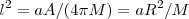
或者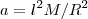，。嗯，这是牛顿公式！貌似我们得出牛顿引力了，而牛顿引力常数与基本面积成正比，这是Planck长度公式。

我觉得，上面的推导与很久以前Jacobson的推导似乎没有多大区别。Erik Verlinde口袋里应该远远不止这点货。

过了三天，Koelman注意到一篇新文章，是另一个人写的：

Equipartition of energy in the horizon degrees of freedom and the emergence of gravity by T. Padmanabhan

我大致看了这篇文章，主要内容就是上面的argument。

预告：下篇博文将介绍我自己的文章，一篇关于暗能量的数据拟合，另一篇关于de Sitter vs metamaterials中Casimir energy的进一步研究。其实这是广告。

附，Koelman的博文 Holographic Hot Horizons