从上学期开始，我一直想用引力即熵力理论找到暗能量的具体形式（当然私心是找到支持全息暗能量的证据），我们没有成功，似乎没有任何人成功了。

一开始，我就觉得Verlinde的想法中闭合的全息屏是最大的障碍，因为要研究宇宙学，不存在任何整体的Killing 矢量，特别是某种宇宙学视界上不存在整体Killing矢量，所以他的想法很难用到宇宙学上。

所以，我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质，所以无法直接研究能量，但可以研究某段时间流过屏的能量。我们摸索了很长时间，后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。

从7月份一直折腾到上个月，我们似乎看到了希望。开学后，谷伟也加入了我们。昨天，我将最后结果贴出来了：

A New Entropic Force Scenario and Holographic Thermodynamics

这个project一共做了四个月左右，终于结束了。

昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上，我已经做了这个工作的演讲。

如果用一句话总结我们的建议与Verlinde的不同，就是，我们建议用Brown-York能量做全息屏上的能量，而不是Tolman-Komar质量，Verlinde假设后者满足能量均分定理（通过爱因斯坦方程，这个假设是正确的），而Brown-York能量一般不满足能量均分。

更一般的，我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息，所以，我们还多了一个数据，就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中，面上只有温度，温度也是由几何给出的。我们的建议虽然不同，但在用到几何上面，与Verlinde并无本质不同。

我们建议的能量有如下的形式：

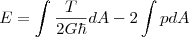
我们看到，非零的面压强破坏了能量均分。

推导爱因斯坦方程的大致过程是，从能量出发

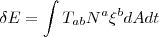
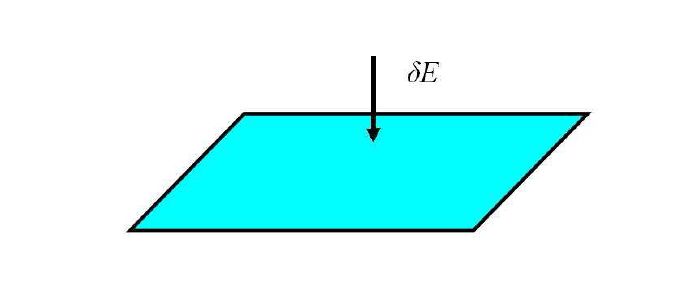
这个能流发生在时空中，根据全息原理，应该等于屏上的能量变化，而屏上的能量变化分两部分，一部分是面密度的变化，另一部分是能量从屏流到屏的其他部分，具体公式就不写了，图示如下：

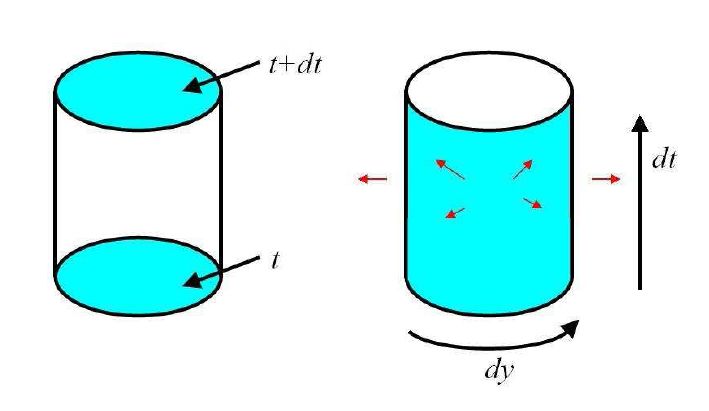
将两个能量变化相等，就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一，开放的屏可以任意小，所以积分方程可以变成微分方程。第二，Verlinde需要温度，而对于任意封闭的面，温度不是恒正定的。第三，既然我们需要用到面上的stress tensor而不是温度，我们可以用别的量取代extrinsic curvature，从而获得其他理论如高阶导数理论。过去我和庞毅证明了，Verlinde理论不能用到高导数理论。

我们的推导与Jacobson相似，他也用了能流，但他的全息屏是类光的，我们的是类时的。他只用到类光屏的面积变化（即熵变化），我们没有引进热力学。但后来我们可以引进热力学，采用Verlinde温度，但熵不由几何直接给出，需要解热力学第一定律。换言之，我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外，类光屏上压强为零，也没有能量从屏流到屏的另一部分现象（所以热力学很简单，任意小的开放类光屏类似一个封闭系统）。

热力学需要单独研究，引进Verlinde温度，以及面压强，甚至化学势（事后看，这是自然的，面的变化自然会导致被激发的自由度的变化），我们研究了一个球对称气体，获得了全息熵。这个全息熵很像Bekenstein熵界，但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵，说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数，这个结果是我们的图像的预言，而Verlinde图像还没有预言。

气体全息熵的导出是我相信这个新建议的主要原因。

全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。

另外，很重要的是，Verlinde图像无法用到热力学上，对于一个气体，很难获得可以接受的熵公式。

我建议大家读我们的文章。

当然，不用说，还有很多要做的研究。